我们经常会碰到测出的振动数据非常像滚动轴承故障，频谱缺与滚动轴承故障频率对应不上。这是为什么呢?下面是CSI一个用户振动这种情况发表的一篇论文，个人觉得总结的相当不错，拿出来供大***分享。

　　一、概述

　　一般情况下，固定型号的滚动轴承在恒定的转速情况下运转时，如满足纯滚动条件，其内圈、外圈、滚动体和保持架等各元件的故障特征频率是不变的，因此，通过振动波形和频谱分析，发现轴承故障并不难，但是当有异物阻碍滚动体转动时，内圈与滚动体将会发生相对滑动，不满足纯滚动条件，滚动体的公转转速将会发生改变，从而导致轴承各元件的故障特征频率也发生相应的改变，这会给轴承的故障诊断带来一定的困难。下面以我司的一台消防稳压泵的轴承故障为例，探讨轴承各元件的故障特征频率改变的原因。

　　二、滚动轴承各元件之间的转速及频率关系分析

　　在正常情况下，轴承各元件之间满足纯滚动条件，它们的转速关系如下[1]：

　　nc= [ni(1-γ)+ no (1+γ)]/2 (1-1)

　　nic= ni-nc= ni- [ni(1-γ)+ no (1+γ)] /2 (1-2)

　　noc= nc - no= (ni -no)(1-γ)/2 (1-3)

　　nb=Dm(ni -no) (1-γ2) /2d (1-4)

　　式中：γ= dcosα/Dm; (1-5)

　　Dm——滚动体中心圆直径，mm;

　　d——滚动体直径，mm;

　　α——接触角，(°)。

　　ni——内圈的转速，r/min;

　　no——外圈的转速，r/min;

　　nc——保持架的转速，r/min;

　　nic——内圈相对于保持架的转速，r/min;

　　noc——外圈相对于保持架的转速，r/min;

　　nb——滚动体的自转转速，r/min;

　　当有杂质或者异物存在，使滚动体转动受阻时，由于摩擦阻力增大，滚动体自转速度nb将会下降为nb1，滚动体上与内圈的接触点瞬时速度也跟着下降，但是，由于内圈的转速ni是不变的，始终等于轴的转速，故内圈与滚动体将会发生相对滑动，这时，滚动体上与内圈的接触点公转转速将变为ni1，保持架的转速也跟着变为nc1，内圈、外圈相对于保持架的转速分别变为nic1 和noc1，轴承各元件的转速关系将会发生如下变化：

　　nc1=[ni1(1-γ)+ no (1+γ)]/2 (1-6)

　　nic1= ni-nc1= ni-[ni1(1-γ)+ no (1+γ)]/2 (1-7)

　　noc1= nc1 - no =(ni1 -no)(1-γ)/2 (1-8)

　　nb1=Dm(ni1 -no) (1-γ2) /2d (1-9)

　　在通常情况下，轴承外圈是固定的，故no=0，而内圈与转轴连在一起，故其转速等于轴的额定转速n，即ni=n;因此，式(1-6)至(1-9) 可写成：

　　nc1=ni1(1-γ)/2

　　nic1= ni-nc1= n-ni1(1-γ)/2

　　noc1= nc1 - no =ni1(1-γ)/2

　　nb1=Dmni1 (1-γ2) /2d

　　由此得出外圈固定的单列滚子轴承各元件的故障特征频率分别是：

　　fc= nc1/60=ni1(1-γ)/(2*60) (1-10)

　　fi= znic1/60=z[n-ni1(1-γ)/2]/60 (1-11)

　　fo =znoc1/60= zni1(1-γ)/(2*60) (1-12)

　　fb = nb1/60=Dmni1 (1-γ2) /(2d*60) (1-13)

　　式中：fc ——轴承保持架的故障特征频率，Hz;

　　fi ——轴承内圈的故障特征频率，Hz;

　　fo ——轴承外圈的故障特征频率，Hz;

　　fb ——轴承滚动体的故障特征频率，Hz;

　　式(1-10)至(1-13)既可用于滚动体与内圈发生相对滑动的条件，也可用于发生纯滚动的条件。滚动体上与内圈的接触点公转转速ni1是影响轴承各元件故障特征频率的关键因素，当滚动体与内圈发生纯滚动时，ni1= n;当滚动体与内圈发生相对滑动时，ni1< n，其大小取决于滚动体摩擦阻力的大小。

　　三、滚动轴承故障特征频率改变的案例分析

　　我司的消防稳压泵是一台电动机驱动的悬臂式离心泵，泵转子由两个滚动轴承支承，泵转速为n=2975r/min，叶轮有5个叶片。正常运行时滚动轴承的振动加速度冲击能量约为2Gs(1G=9.8mm/s2)，但在某次检测时测得泵非驱动端滚动轴承的振动加速度冲击能量达到20Gs，比正常运行时***出10倍，为此，对该轴承进行了振动频率分析。

　　***先，计算轴承各元件的故障特征频率。轴承型号为SKF6309，轴承的几何尺寸如下：中径 Dm=72.5mm， 滚珠直径 d=17.5mm，接触角α=0°，滚珠数z=8;当滚珠与内、外圈之间发生纯滚动时，ni1= n，由式(1-10)至(1-13)可知，轴承各元件的故障频率计算如下：

　　泵的转速频率：fn=n/60=49.58Hz

　　轴承内圈的故障特征频率：fi=1/2*n/60*(1+dcosα/ Dm)*z=246.20Hz

　　轴承外圈的故障特征频率：fo=1/2*n/60*(1-dcosα/ Dm)*z=150.46Hz

　　轴承滚动体的故障特征频率：fb=1/2*n/60* Dm /d*(1-d2cos2α/ D2m) =96.72Hz

　　轴承保持架的故障特征频率：fc=1/2*n/60*(1-dcosα/ Dm) =18.81Hz

　　其次，分析测得的振动波形和频谱图。图1(a)和(b)为水平方向测得的加速度信号时域波形图及其直接进行快速傅立叶变换(FFT)后得到的频谱图，其中频谱图(a)中在1000～3500Hz范围内出现了很丰富的频率成份，其中******幅值0.74Gs 出现在3083.4Hz处，这些频率属于轴承元件的固有频率，说明轴承已经出现故障;再看时域波形图(b)，可以看出有0.02s(49.58Hz)的间隔频率，即转速频率fn，且冲击能量水平(峰峰值)达到20Gs;但是从波形图和频谱图都无法看清楚，具体是轴承的哪个元件出现故障。

　　

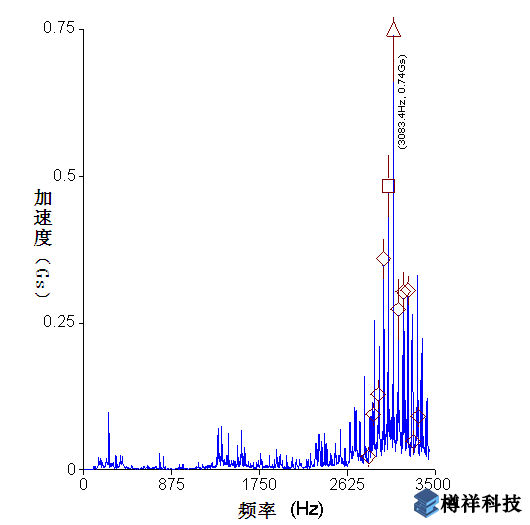
　　图1(a)加速度频谱图

　　

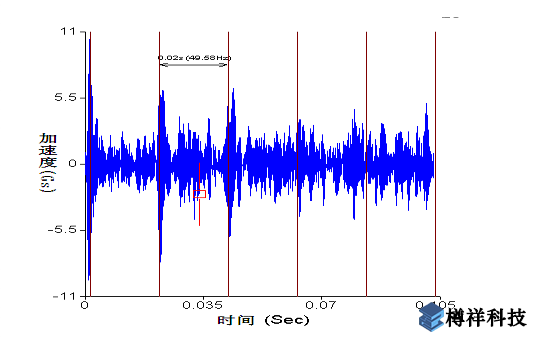
　　图1(b)加速度时域波形图

　　为了看清楚轴承的具体故障根源，采用了PeakVue诊断技术重新采集了振动数据。PeakVue是一种监测轴承故障的新方法，该方法着眼于分析由于金属与金属之间的冲击或摩擦形成的应力波信号。当滚珠通过缺陷区时，由于油膜突然中断，导致金属直接碰撞，从而产生应力波。应力波是一种非常短暂的脉冲信号，它属于低能量信号，隐藏在诊断频谱底层的背景能量中，如前面所述，用常规的振动信号采集和频谱分析难以发现。而PeakVue的原理是***先以极***的采样频率(100KHz)采样，保证能够捕捉到***频的应力波信号，采集到的时域数据通过***通滤波，去除低频信号，再通过二次采样等信号处理，仅保留幅值较***的峰值，达到突出***频但具有较***幅值的应力波冲击信号，从而能更早期、更明显地诊断故障的根源。

　　图2(a)~(c)是测得的PeakVue时域波形和频谱图，其中图(a)是频谱图，该图中显示出主要冲击能量来自于转速频率fn (49.58Hz) 及其谐波(2fn，3fn，4fn，5fn)，同时出现了转速倍频的边带频率6.89 Hz;此外还出现了6.89 Hz的频率及其谐波;图 (b)是时域波形图，该图出现了转速频率fn的周期信号，为了更清楚的显示重复出现的周期信号，对时域波形图进行自相关处理，即将波形中的其中一半与另一半进行关联比较，当时域波形中出现周期信号时，两组信号的相关性将使得到的波形中周期信号更加明显，同时削弱非周期性冲击信号。 通过自相关处理后，得到了图 (c)所示的自相关时域波形图，该图清楚的显示出0.02s(49.58Hz)的间隔频率，即转速频率fn，同时该频率被另一个周期为0.14s(6.89Hz)的信号所调制。

　　

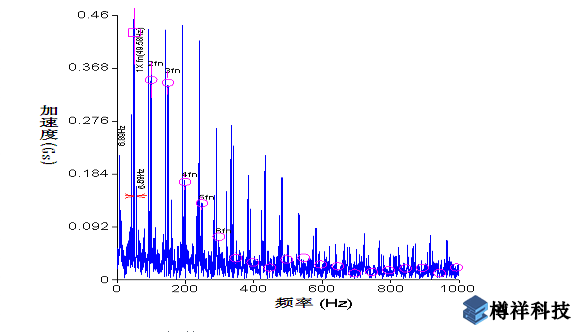
　　图2(a)PeakVue频谱图

　　

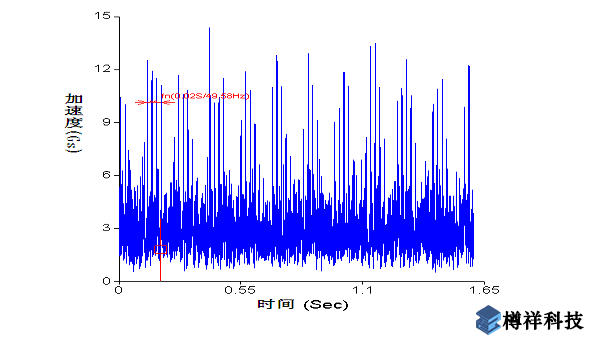
　　图2(b)PeakVue时域波形图

　　

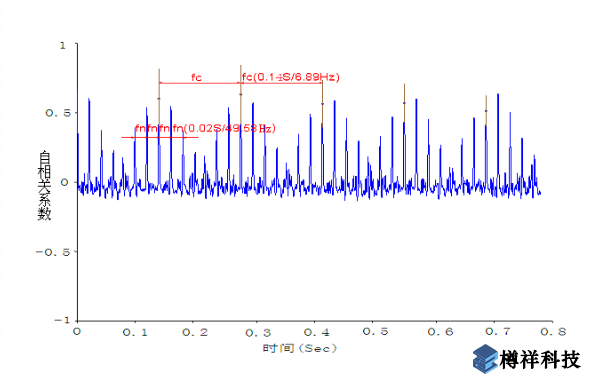
　　图 2(c)自相关处理后的PeakVue时域波形图

　　显然，不管是时域波形还是频谱图，均没有出现前面计算得出的任何一个轴承元件的故障特征频率。但是由于振动冲击能量很大，所以决定对该泵进行解体维修，解体后发现轴承保持架已断裂，并且有一块碎片残留在其中一个滚动体与外圈之间(如图3所示)。由此可作如下分析：由于有保持架碎片的存在而导致滚动体的摩擦阻力急剧增大，引起滚动体自转速度下降，其上与内圈接触点的瞬时速度也跟着下降，但内圈转速始终等于轴的转速，其上与滚动体接触点的瞬时速度也不变，这样内圈与滚动体就发生了相对滑动，保持架的频率fc由18.81Hz变成了6.89Hz，由式(1-10)可知滚动体上与内圈接触点的转速ni1就变为1089.7r/min，由式(1-11)至(1-13)可知轴承各元件的频率也发生了相应的改变，即fc= 6.89Hz，fi= 341.56Hz，fo = 55.12Hz，fb = 35.43Hz。对照 图2 (a) 中的频谱图，除保持架故障频率外，其它轴承元件的故障频率均不明显，与实际情况相符;此外，由于保持架碎片的存在，导致转轴出现偏心，引起1倍基频49.58Hz的增大;又由于从轴承承载区到非承载区，其径向游隙是逐渐变化的，因此，保持架每旋转一周，保持架碎片也跟着旋转一周，转子偏心量也会随之变化，也就是说，1倍基频49.58Hz被保持架频率6.89Hz所调制，这与在PeakVue频率图上49.58Hz及其倍频出现6.89Hz的边带是相符的。

　　四、结论

　　从以上案例分析可知，当有杂质或者异物存在，使滚动体转动受阻时，由于摩擦阻力增大，滚动体自转速度将会下降，滚动体上与内圈的接触点瞬时速度也跟着下降，而内圈的转速是不变的，始终等于轴的转速，故内圈与滚动体将会发生相对滑动，不满足纯滚动条件，滚动体的公转转速将会发生改变，这就是轴承各元件的故障特征频率发生改变的原因。