当使用振动数据时，特别是与建模系统结合使用时，测量数据通常需要作为加速度，速度和位移。有时，不同的分析组需要以不同的形式测量信号。显然，即使我们能够同时测量所有三个也是不切实际的。从物理上讲，将三种不同类型的传感器放在同一个地方几乎是不可能的。

加速度计有各种类型和尺寸，有很多选择。有些类型可以测量到DC（0Hz），其他类型可以测量***冲击负载等等。

真正的测速仪是非常罕见的，但他们确实存在。基于线圈和磁体方案的一个有趣的类是自供电的。

直接位移测量并不罕见。有些使用应变计，但许多其他人使用电容效应或感应射频机制直接测量位移。电容和电感类型的优点是它们是非接触式探针并且不会影响局部质量。

但无论如何它并不重要，因为如果我们测量加速度，速度或位移，那么通过明智地使用积分或微分来转换它们肯定是简单的数学，如下所示。

测量 信号 类型	手术	结果
移位	区分	速度
移位	双重区分	促进
速度	区分	促进
速度	整合	移位
促进	整合	速度
促进	双重整合	移位

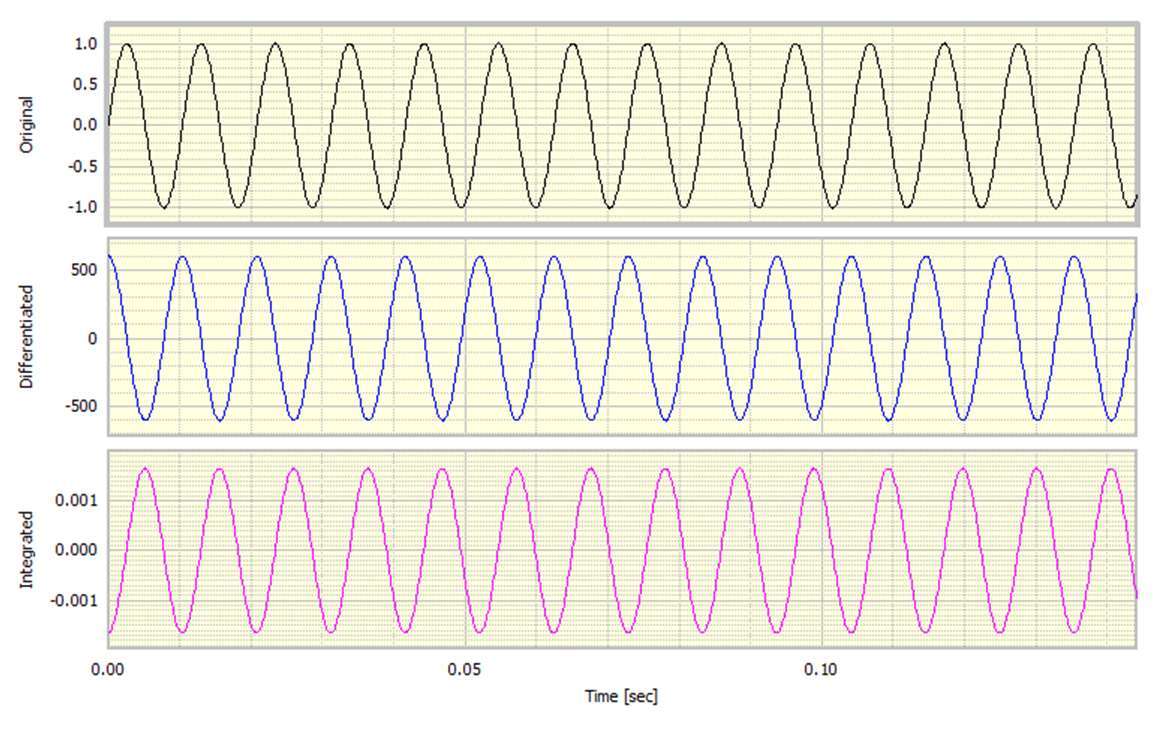
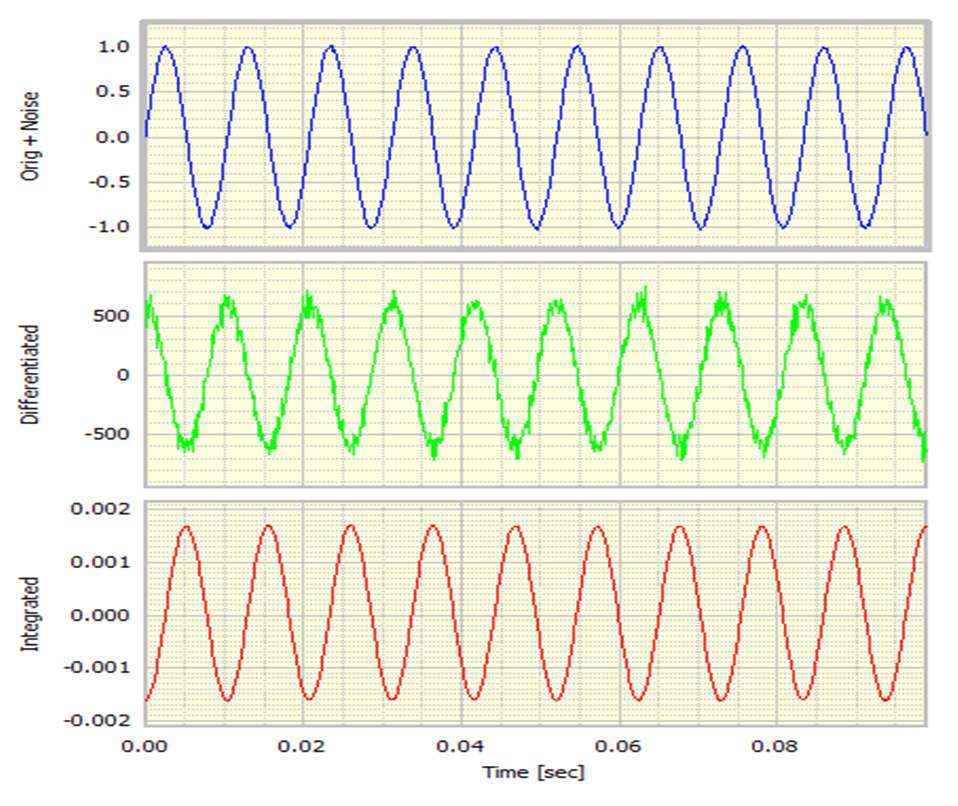
现在让我们用经典的正弦波信号来看这个，看看区分或积分它的效果。为了避免其他副作用，该示例使用单位幅度的96Hz正弦波，以8192个样本/秒生成32768个样本。将这些视为时间历史和频率的函数是有用的。也就是说，使用DATS工作表处理原始生成的正弦波，如图1所示。

看一下波形的一部分，我们得到了一个经典的结果，如图2所示。

在数学术语中，如果那么差分是，并且积分是C所谓的“积分常数”。在这两种情况下，有90°的相移0，其接通正弦成余弦。 差值乘以。积分除以，也被否定并且已经添加了偏移，在这种情况下是合成幅度的一半，导致积分信号完全为正。例如，如果原始信号表示加速度，那么积分信号就是速度，显然我们不希望它完全是正的。该积分常数是标准积分方法的假象。

对于数学倾向，它是执行通常被称为不定积分的结果。解决方案非常简单。在进行基于标准时间的积分之后，我们应该自动将结果减小到具有零均值。也就是说，我们确保没有残余的DC偏移。计算过程被修改为包括该动作，结果如图3所示。注意积分信号如何正如我们所期望的那样是正面的和负面的。

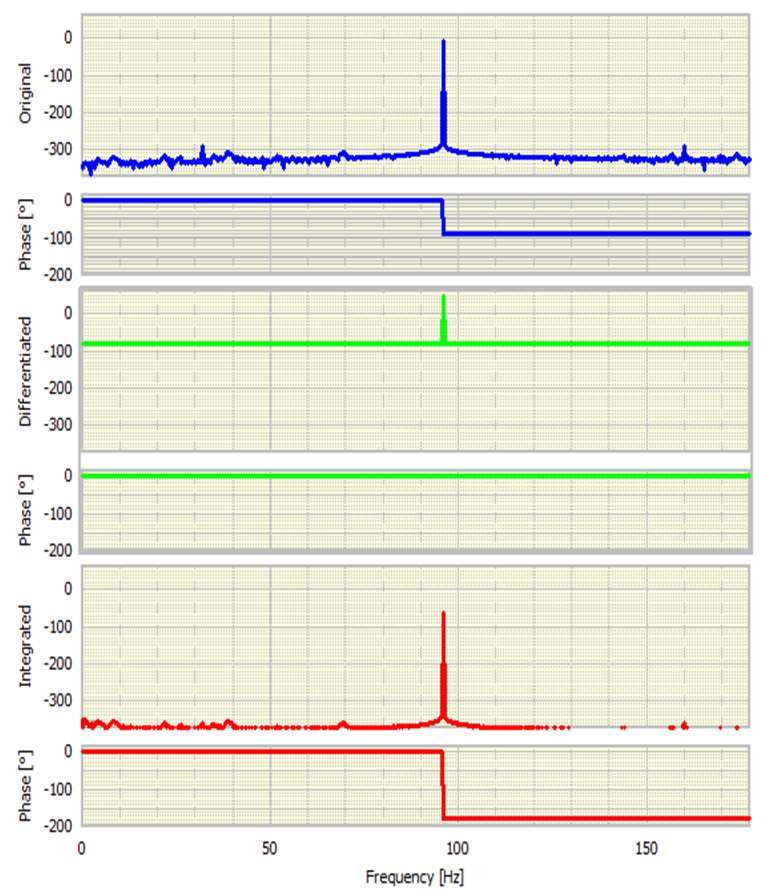
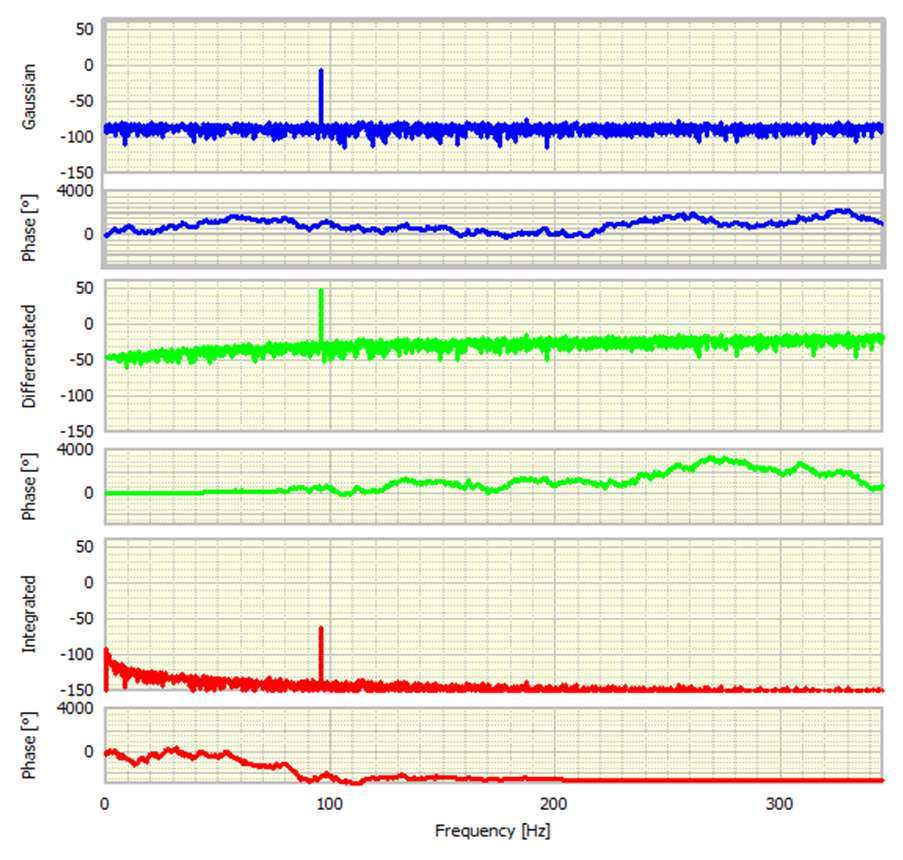
查看三个信号的傅立叶变换也很有趣。这些在图4中以模量（振幅）和相位形式示出。模数以dB表示，相位以度为单位。

***先看相位，原始正弦波的相移为-90 0。这完全符合预期，因为FFT的基础实际上是余弦。差分信号的相位变化为零，因为它现在是纯余弦。积分信号具有180度相位变化，表示它是负余弦。

原始信号的动态范围远远超过300 dB，这并不奇怪，因为它是在双精度软件中生成的。这相当于50位精度ADC！集成信号显示出类似的动态范围，但***初看起来令人惊讶的是，差分信号已经失去了动态范围的一半。我们稍后会回到这一点。

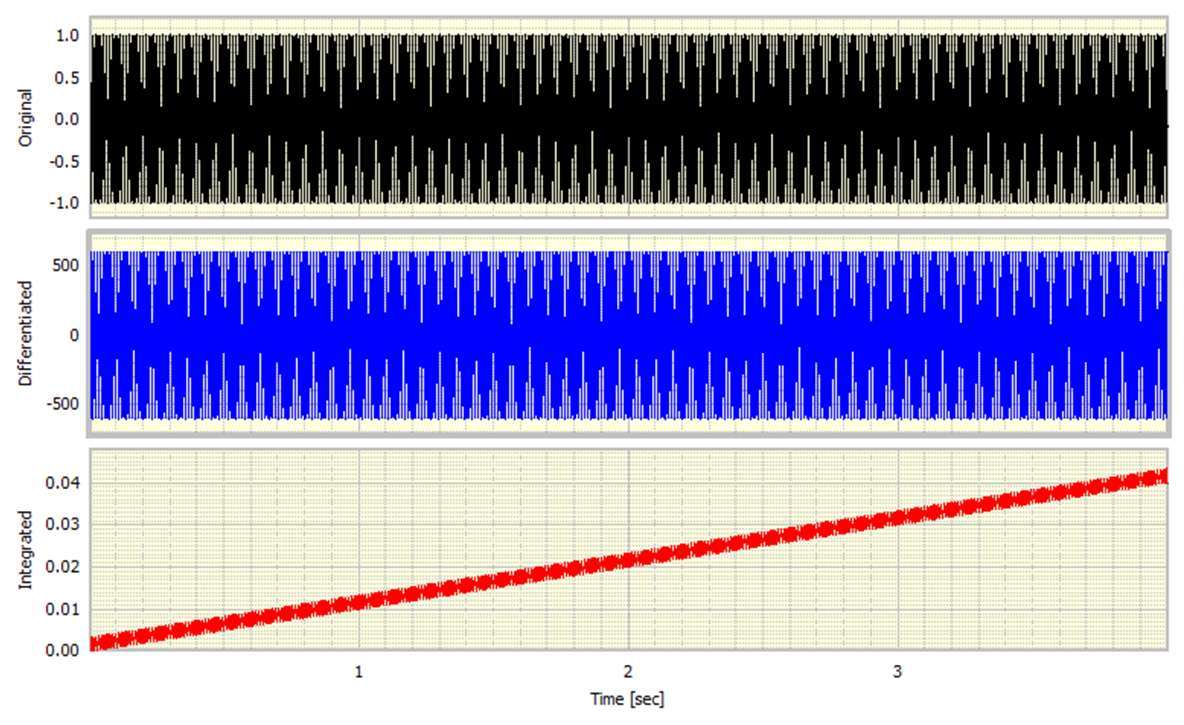
在许多数据采集系统中，小DC偏移并不罕见。有些提供交流耦合（***通滤波）以***小化任何偏移。这会如何影响合成信号？为了说明这一点，将0.01（幅度的1％）的小DC偏移添加到原始正弦波信号中，结果如下所示。

对原件的影响基本上不明显。类似地，差分信号如预期的那样不变。但是对集成信号的影响是非常显着的。小的DC偏移产生了巨大的趋势。我们在4秒内积累了0.01常数，累积的“漂移”为0.04。潜在的集成信号仍然很明显，并叠加在这个漂移上。

我们如何避免这种情况？只需将输入减少为零均值，通常称为正规化。

注意，在这个时刻，当我们进行微分时，我们不必对初始信号做任何事情，但是我们必须在积分之前去除任何DC偏移以防止“漂移”并且还从集成信号中去除DC偏移消除整合的常数。因此，在这个阶段，人们可能会试图得出结论，使用差异化方案可能是***好的前进方式。但是，当我们添加噪音时情况会发生变化。

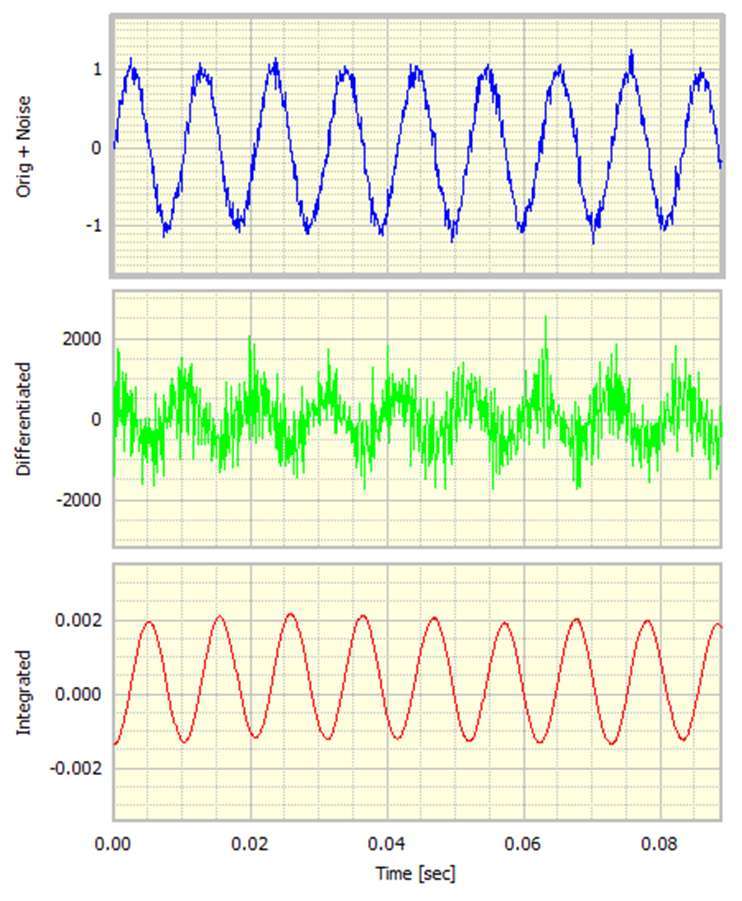
***先，在原始正弦波上添加了一个小的随机噪声信号。

原始信号上的眼睛无法辨别噪声，但差分信号变得非常嘈杂。集成信号保持平滑。然而，我们可以很好地识别主导频率。

如果检查噪声信号的相位，可以看到它现在到处都是，并且基本上不再有任何值。使用自动相位展开，如果相位已经在360 °范围内显示，则它将完全填充相位图区域。

具有附加噪声的原始信号的动态范围约为90dB，差分和积分信号具有相似的范围。也就是说，增加的噪音主导了范围。

要注意的另一个方面是集成信号上的噪声的背景电平在较低频率上升。这被称为1 / f噪声（一个超过f噪声）。这设定了有效的较低频率限制，低于该频率限制，集成不再可行。

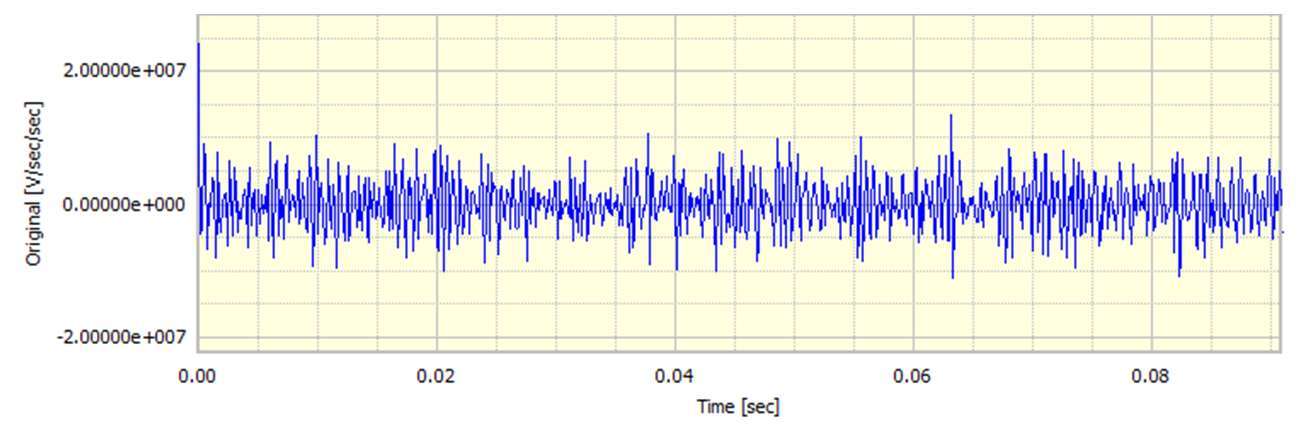
为了强调噪声的挑战，下一个例子具有非常大的噪声含量。

 

这里原始信号的噪声很明显。差分信号实际上是无用的，但集成信号相对干净。为了说明这一点，嘈杂的正弦波被区分了两次。结果如下所示。原始正弦波的所有痕迹似乎已经消失，或者更确切地说，已经在噪音中消失了。

结论现在很清楚。如果没有特殊情况，那么经验表明***好用加速度计测量振动。但是，如果需要对速度或位移进行任何积分，则需要注意去除极低频率。

***后一点，为什么差异化要比整合更吵？答案是差异是一个减法过程，在它的基本水平上，我们取两个连续值之间的差异，然后除以样本之间的时间。两个相邻的数据点的大小通常非常相似。因此，差异很小并且准确性会降低，然后我们除以通常是小的时间差，这往往会放大任何错误。在水獭手上整合是另外的。由于任何宽带噪声往往是连续的，不同的符号，然后噪声抵消。

当然，这篇文章并不能说明整个故事，但它提供了一个非常简单的良好实践指南。