转子振动系统本身并不完全是线性的，由于用线性振动理论能比较简便地研究和解决旋转机械系统的主要故障，所以在精度允许的情况下，可以把非线性振动问题线性化，作为线性振动来处理。虽然现阶段非线性理论研究还不尽完善，近年来发现，在非线性系统中还会出现貌似随机而对初始条件极为敏感的运动，称为混沌，“蝴蝶效应”说明了非线性的不可预知性，但根据现有的一些研究成果，一些无法用线性振动理论来解释的异常振动现象，用非线性振动理论阐明故障机理，却很方便。

　　如果动力载荷使结构或机器的一部分超出材料弹性范围的变形，那么产生的运动为非弹性反应，通常情况下当系统偏离平衡位置较大时才考虑非线性问题，微振情况下可认为是线性的，但有时位移很小，也须考虑非线性问题。造成非线性的因素，通常是阻尼项或刚度项出现非线性，比如轴承的油膜，其刚度、阻尼与厚度是非线性的，配合间隙与摩擦、材质不均引起的阻尼与速度是非线性的，还有裂纹、大变形产生的非线性刚度。在机械振动系统里阻尼随属于强非线性，但除共振外，其对振动影响非常小，基本可以忽略不计。下面主要介绍一些非线性振动的特点。

　　1.线性系统中，由于阻尼的存在，自由振动是逐渐衰减的，只有在干扰力的情况下才有周期振动，而非线性系统，有阻尼力而无干扰力时也会发生周期振动，如自激油膜震荡;

　　2. 线性系统中，固有频率与起始条件、振幅无关，而非线性系统中，与振幅有关，同时非线性系统的振动三要素也和起始条件有关;

　　3. 线性系统中，激振力为简谐振动时，系统响应也必为简谐振动响应，而非线性时，波形周期与激励相同，但响应是非正玄的，而是包含了激励中不存在的谐波成分，如图，非线性响应波形变成了一个尖波，其形状随非线性程度而变，当出现强非线性时，波形可能变为平顶波。

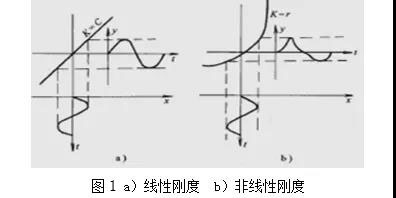
　　4. 非线性系统中会出现次谐波和超谐波，大的阻尼可以抑制次谐波的出现，但只能减小超谐波的幅值;在某种特定的运动状态下，可能还会产生次谐波共振和超谐波共振。

　　5.非线性系统中叠加原理将不再适用，受迫振动不等于各谐波振动的叠加，而且非线性系统的平衡位置不止一个而可能有多个;复杂的非线性系统在一定条件下还会产生突变、分岔、混沌等现象。

　　6. 固有频率随振动幅值而变化，线性振动系统的固有频率只与系统的固有特性(k、m)有关，是一固定数值。而非线性振动系统则不同，其固有频率随振动系统的振幅大小而变化，对于硬弹簧，随振幅的增大而提***，对于软弹簧，随振幅的增大而提***而减小。在一定情况下这个特点可以解释与给定临界不符发生的强振现象。

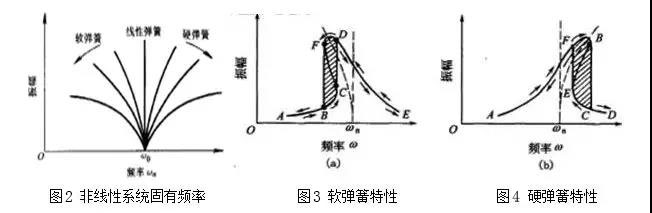
　　7. 振幅跳跃现象， 具有非线性弹性的机械系统，在周期激振力作用下，振动可用强迫振动的基本成分ω与其***次谐波分量之和来表示。据此可得到不同阻尼特性和振幅下的共振曲线，如图所示。

　　图(a)为软弹簧的情况，图(b)为硬弹簧的情况。在图(a)中，如将激励频率慢慢增大，振幅将沿曲线AB变化;在BC之间具有三个平衡点，而CF之间的平衡点是不稳定的平衡点。因此，从B移向C，一过C点就突然跳跃到D，然后进到E点，振幅发生突变。如将激励频率慢慢减少，从E下降的情况，经过的路程是从EDF跳跃到BA。在图(b)中，振幅也同样发生突变，这种现象称为振幅跳跃现象。相位也有相同的跳跃现象。

　　8. 组合共振，在非线性系统中，若有两种不同频率ω1和ω2的激振力作用于系统，会产生新的频率成分，即它们的和(ω1+ω2)、差(ω1-ω2)。由于非线性系统的固有频率随振动而变，当新的频率成分与固有频率一致时，会引起共振，称为组合共振

　　9.频率俘获现象，干扰力频率接近自振系统固有频率ωn到一定程度时，所激起的振动中只包含干扰力频率而自振频率被俘获的现象。17世纪，C.惠更斯已观察到：快慢稍微不同的两只时钟，挂在同一壁板上会保持同步计时。当ω-ω2的绝对值小于某个阈限时，拍频就突然消失，只剩下频率为ω的输出，即自振和受迫振动发生同步，或者说自振频率被扰频所俘获，因而这一现象也称为频率俘获，同步现象不仅出现在扰频和自振频率相近的区域，在一定条件下，也可出现在扰频的整分数倍和自振频率相近的区域，这种现象称为亚谐同步。